一言。
以下は、2006年初頭に認めたものです。
まだ数検3級も取得してなかった当時書いた内容ですので、
拙い限りではありますが、この度当サイトにアップすることにいたしました。
一言。
以下は、2006年初頭に認めたものです。
まだ数検3級も取得してなかった当時書いた内容ですので、
拙い限りではありますが、この度当サイトにアップすることにいたしました。
![]()
統計ソフト「R(アール)」を使ってみた体験記です。
でも、統計をやってみたわけではありません…。 (詳しくは以下。)
本コーナーは、最後にオチが付きます。
途中経過には間違いがありますので、その旨ご注意ください…。
(オチは、このページ最後の方にあります。)
![]()
背景 会計の本を読んでいたら、こんな問題が出てきました。 P/L(損益計算書)の各項目が空白になっていて、そこに数値を入れていくような問題だったのですが、その中で特に 「期首商品棚卸高」と「当期商品仕入高」が、どうにも算出できません…。 どなたか数学にお強い方、教えてください。 お願いします。 分かっているのは、以下の内容です…。 当期純利益 = 1,932,000円 期末商品棚卸高 = 1,264,800円 売上総利益率 = 30% 売上純利益率 = 8% 商品回転率 = 15回転 ざっとこんな感じです。 この情報を元に、「売上高」・「期首商品棚卸高」・「当期商品仕入高」・「売上総利益高」などを求めてみてください。 (参考) 売上総利益率(粗利率)=売上総利益÷売上高×100(%) 売上純利益率=当期純利益÷売上高×100(%) 商品回転率=売上高(下代)÷{(期首商品棚卸高+期末商品棚卸高)÷2} 私はこの問題を解いていくうちに、「これは連立方程式を作らないとダメじゃないの?」と思いました。 それがですね。 いくら解こうにも解けない。(^^;) 私が連立方程式の解き方を忘れてしまったのか・・・、それともこの問題が難しすぎるのか・・・。 途中までは、自分にも出来るんです。 例えば「売上高」なら、1,932,000円÷8×100で出ますね。(24,150,000円) これが出れば、次の「売上総利益高」もすぐ出ます。(「売上高」×30%=7,245,000円) ・・・ここまでは何てことないのですが、残る「期首商品棚卸高」と「当期商品仕入高」が、どうにも算出できません…。 商品回転率が15とあります(これを求める公式は 仕入÷平均在庫 です。)が、平均在庫は (期首在庫+期末在庫)÷2 で求めることになっています。(一応…。) さて。 このあとどうします?? 方程式 その1 …在庫等式(期首棚卸+当期仕入-期末棚卸=売上原価)に当てはめると…。 期首棚卸+当期仕入-1,264,800円=24,150,000円-7,245,000円 (売上原価=売上高-売上総利益 なので。) …ここで期首在庫をx、仕入をyとおき、さらに上記の式を変形させると、 x + y = 18,169,800 ・・・・・ ① ざっとこいつが、「方程式①」です。 方程式 その2 …商品回転率を求める公式(仕入÷在庫)から、 仕入 ÷ 平均在庫 = 15 …ここで期首在庫をx、仕入をyとおくと、 →y ÷ {(x+1,264,800円)÷2} = 15 さらに、両辺に2を掛けて、 2y = (x+1,264,800円)×30 ↓ 30x - 2y = -37,944,000 ・・・・・ ② こいつが、「方程式②」です。 私だって、ここまでは出来ます…。 さあ~! ここまで来れば、あとはこの連立方程式を解くだけ。 ・・・・・でも・・・・・。 この先が…、ややや、解けない解けません。(笑) わからんなぁ~。 数値がでか過ぎて、机上では思うように解けない。 「くそ~、一次の連立方程式も解けんとは! 我ながらなんとも…。」 そんなわけで…、参りました・・・・・。 数学計算ソフト 「MuPAD」という、オープンソースらしき数式計算ソフトがあります。 これが無料で使えるものなのか、それとも安いだけなのか、定かではなかったのですが、自分で方程式が解 けないなら「数学ソフト」をダウンロードしようと思い、検索してみました。 いろいろ調べてみたところ、わりと最近“無料バージョンが廃止”になったようでした。(^^;) ・・・・・。 仕方が無いので、他のをあたってみました。 実は、先日ご紹介した「Python」なども、パソコン電卓として十分な性能を持っているのですが、さすがに「方程 式」には対応していないようです…。 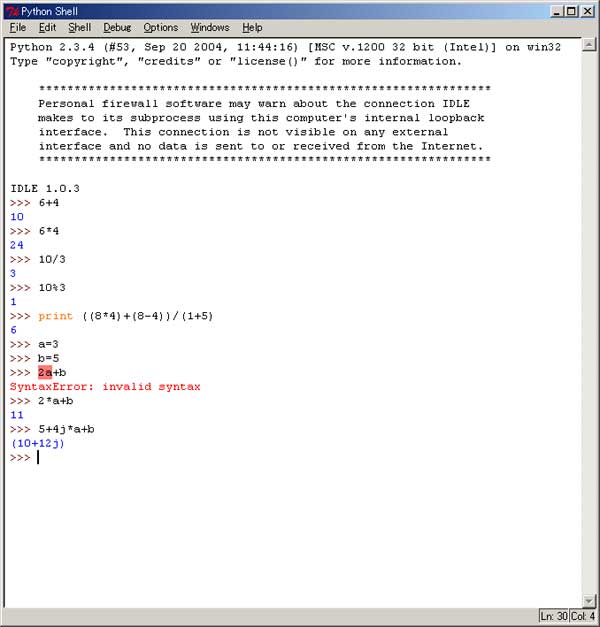 “*”は“×”の意味。 “/”は割り算ですね。 “%”は余りです…。 上記のように、変数も使えます。 あと、“j”は虚数です…。 「Python」は虚数が扱えるというのが強力なウリのようで、大概の「Python本」には このことが載っています。 が、その恩恵を受ける人が全世界にどれほどいるのかについては、定かではありません・・・・。 しかしそれにしても、方程式に対応した電卓くらい、世の中にあって良かりそうな気がします…。 実社会でも案外、用途があると思うのですが。 「関数電卓」があるというのに、「方程式電卓」がなぜ、無いのでしょうか…? 「R」 統計のフリーソフトに、「R」というものがあります。 主に統計解析用のソフトなのですが、何とこいつを使って、連立方程式を解くことが出来るようです。 ダウンロードはココから出来ます。(無料です。) 例えば、Version2.2.1のWindows版なら、“R-2.2.1-win32.exe”をダウンロードします。 すみません。 細かな手順は、ちょっと面倒くさいのではしょります。 で、ちょっとやってみました。 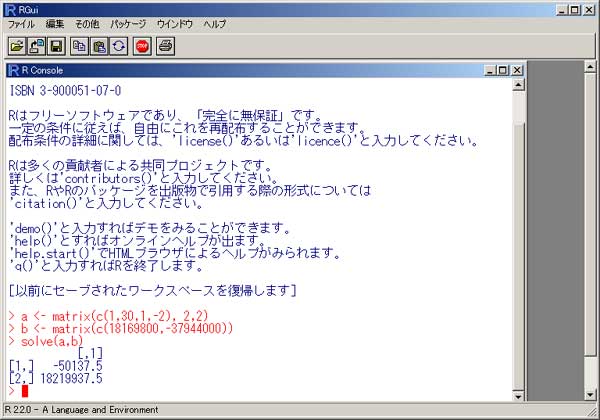 入力したのは、 > a <- matrix(c(1,30,1,-2), 2,2)[ENTER] > b <- matrix(c(18169800,-37944000))[ENTER] > solve(a,b)[ENTER] の3行。 何のことかと言うと…。 x + y = 18,169,800 ・・・・・ ① 30x - 2y = -37,944,000 ・・・・・ ② 上記の2式を、左上から“N”の字のように数値(定数)部分を読んでみてください。 1、30、1、-2 となっていますね。 これが1行目の“a <- matrix(c(1,30,1,-2), 2,2)”に該当します。 (最後の“2,2”というのは、2元2式の方程式であることを示すようです…。 ・・・『ようです。』などと書いているのは…、私も試行錯誤しながら使っているからデス。(^^)) 別解 上のやり方では、“N”の字のように定数を“縦”式に並べていましたが、“横”式にすることも出来ます。 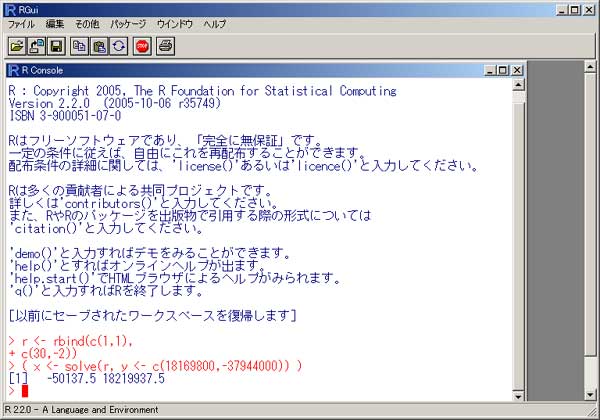 入力したのは、 > r <- rbind(c(1,1), + c(30,-2)) > ( x <- solve(r, y <- c(18169800,-37944000)) ) の3行。 以下、ご説明しましょう。 x + y = 18,169,800 ・・・・・ ① 30x - 2y = -37,944,000 ・・・・・ ② 上記2式を、係数について横に並べます。 1,1 30,-2 18169800,-37944000 (右辺だけは、なぜか縦式です…。) さて…。 結果が出ました。 答えは、x(期首在庫)が “-50,137.5円” 、 y(仕入)が “18,219,937.5円” となりました。 なるほど確かに、上の①式にも②式にも該当しますねぇ! x + y = 18,169,800 = -50,137.5 + 18,219,937.5 30x - 2y = 30×(-50,137.5)-2×18,219,937.5 = -37,944,000 = -1,504,125 - 36,439,875 ひゃー! こりゃスゴイもんだ…。 これにて一件落着~!! かと思いきや、 なんで期首在庫がマイナスになんねん!? なんで仕入と在庫に“少数点以下”がつくねん!? という事態に。。。。 「おかしいなぁ~。」 おかしいので、本の解答を見ました。 それによると、正答は「期首在庫」が989,200円、「当期仕入」が17,180,600円となっていました。 残念なことに、この本には“答え”だけが載っていまして、“求め方”が載っていないと言う・・・。 (実はそれで困ってたのです…。) 上記正答に基づいて、「商品回転率」を逆算してみますよ。 17,180,600円÷{(989,200円+1,264,800円)÷2}= ・・・・・ 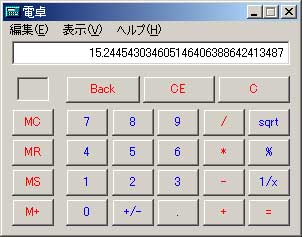 出てきた答えは 15.24454・・・。(こういうのを、無理数と呼ぶんでしたか。) 問題にあった「商品回転率が15」という所与の値は、何と正確な数値ではなく、アバウトのことだった のですね…。 “アバウト15回転”なんていう方程式を…、一体どうやって解けば良いのでしょうか? y ÷ {(x+1,264,800円)÷2} ≒ 15 → 2y ≒ (x+1,264,800円)×30 → 30x - 2y ≒ -37,944,000 ・・・・・ ②’ (注:“≒”は“機種依存文字”になりますので、本当はあまり使いたくなかったのですが。) ???? ・・・・・・・・・・ますます解らなくなってしまいました。 「期首在庫」が989,200円、「当期仕入」が17,180,600円。 どうやって求めるの? というわけで、せっかくの統計解析ソフト「R」が、何の役にも立ちませんでした・・・・。 ところでこのソフト、「2次」の連立方程式は解けるんだろうか…? よく分かりません…。 ああ、間違えた・・・。 商品回転率は、仕入÷在庫じゃなかった…。 売上原価÷在庫でした。(^^;) ・・・・「売れたものの原価」でなきゃ。 ただそれだけのことでした。(笑) 売上原価(24,150,000円-7,245,000円)÷平均在庫=15 なんだから、 平均在庫=1,127,000円 {期首(x)+期末(1,264,800円)}÷2=1,127,000円 で、・・・ x = 989,200円。 出ました。 ここでもう一度在庫等式(期首棚卸+当期仕入-期末棚卸=売上原価)を用いて、 989,200円+当期仕入(y)-1,264,800円=24,150,000円-7,245,000円=16,905,000円 y = 17,180,600円 ・・・・・苦笑。 結局、連立方程式なんて全然、いりませんでした。 お恥ずかしい限りでございますデス。(*^^*) まったくどうしようもないですねぇー。 単なる勘違いでした・・・・。 お騒がせを。 間違えた照れ隠しの意味で、ちょっと「売上原価」関連の小噺を・・・。 「費用収益対応の原則」という原則があります。 これは、『“売れた商品”の販売価格から“売れた商品(のみ)の仕入れ価格”を差っ引いて、利益を算出する。』 というルール。 売上があって初めて「売上原価」が計上される、ってことです。 逆に言うと、売れ残った商品の仕入原価(or製造原価)は、「売上原価」に入らないんですね…。 もう少し解説しますと、 商業の場合、例えば前期繰越商品が25,000円、期末商品が10,000円、当期仕入が70,000円であったとすると、 売上原価 = 25,000 + 70,000 - 10,000 = 85,000 となります。 (在庫等式より) ここで「期末棚卸の10,000円」とは、要するに「売れ残り」のことです。 これより、「売れ残り分の仕入代金」を差っぴいて「売上原価」を算出していることが見て取れます。 製造業で説明した方が分かりやすい。 製品売上時の仕訳は、例えば以下の2つのようになります。(必ず2行要ります。) 現 金 7,500 | 売 上 7,500 ・・・ 販売価格で 売上原価 3,500 | 製 品 3,500 ・・・ 製造原価で でもって、販売価格と製造原価の差額(7500-3500)から、粗利が判明します。 もしも製品が売れ残った場合、その製品の製造原価は「売上原価勘定」(費用)には振り替えられず、「製品勘定」(資産)のままとなります。 売れて初めて、「売上原価」に振り替えられます。 (これを言い換えますと、“売れ残った商品の製造原価は、「売上原価」に入らない”)ということ。 上の等式を製造業向けに加工すると、期首製品棚卸 + 当期製品製造原価 - 期末製品棚卸 = 売上原価 となり、 言葉は似ていても、“「当期製品製造原価」(「製造原価報告書」に示す当期の実製造コスト)と「売上原価」(売れた分の製造原価)では 全く別もの”、であることが分かります。(上の行のリンク先 大元) 実のところ、真面目に考えれば考えるほど、「仕入(当期製品製造原価)」と「売上原価」ってごっちゃになってきます…。 「売れ残り分」を「売上原価」に含めないとなると、当然のことながら、「利益」は実際より大きく見えてしまうでしょ。 P/L(損益計算書)の「売上原価」項目は、こうしたルールで計上されています。 これが、「費用収益対応の原則」…。 何でこんな会計方式がまかり通っているのかと言うと、それはその方が、国が企業から税金をたくさん徴収出来 るからです。 法人税は、利益に対し百分比で徴収されるので、会社の利益額が大きいほど、税額も大きくなる。 それで、(実際よりも)利益額が大きく見えるこの会計制度を維持した方が、政府の税収が期待できるわけです。 けれど、こんな基準で利益を計上していると、経営を見誤る元となります。 俗に言われる“黒字倒産(利益が出ているのに会社が潰れる。)”とは、こうしたことが原因で起こります。 そこで、(「全部原価」を「変動費」と「固定費」に分ける、)「直接原価方式」が、強く求められています…。 その後、(「何を今更・・・。」ではありますが、)連立方程式の解法を復習してみました。 (こんな方程式も解けんでは恥ずかしい。) ・・・どうやら私は、「代入法」のみ記憶していて「加減法」を失念していたようです。 解き方はこう。 x + y = 18,169,800 ・・・・・ ① 30x - 2y = -37,944,000 ・・・・・ ② xかyのどちらかを、足すか引くかして消してしまうのが「加減法」の極意(?)です。 例えば、 x + y = 18,169,800 ・・・・・ ① この式の両辺に2を掛けます。 2x + 2y = 36,339,600 ・・・・・ ①’ そいでもって、①’と②の式を、縦に足し合わせます。 2x + 2y = 36,339,600 ・・・・・ ①’ 30x - 2y = -37,944,000 ・・・・・ ② 32x + 0 = -1,604,440 すると、上手い具合にyが消えますね。 これをxについて解くので、両辺を32で割り算し…、 x = -50,137.5 あとは、これを①式に代入して、 -50,137.5 + y = 18,169,800 y = 18,219,937.5 となりました。 (その後) >>>>> 加減法も知らない自分が恥ずかしくなり、 その後一念発起して、「数検3級」を取得いたしました。(^^) というわけで、やっぱり…。 せっかくの統計解析ソフト「R」が、何の役にも立ちませんでした…。 でもまあ…、「R」で連立方程式の使い方が分かったので、よしとします。 2006年9月 追記 その後、「Maxima」というソフトで連立方程式を解きました。 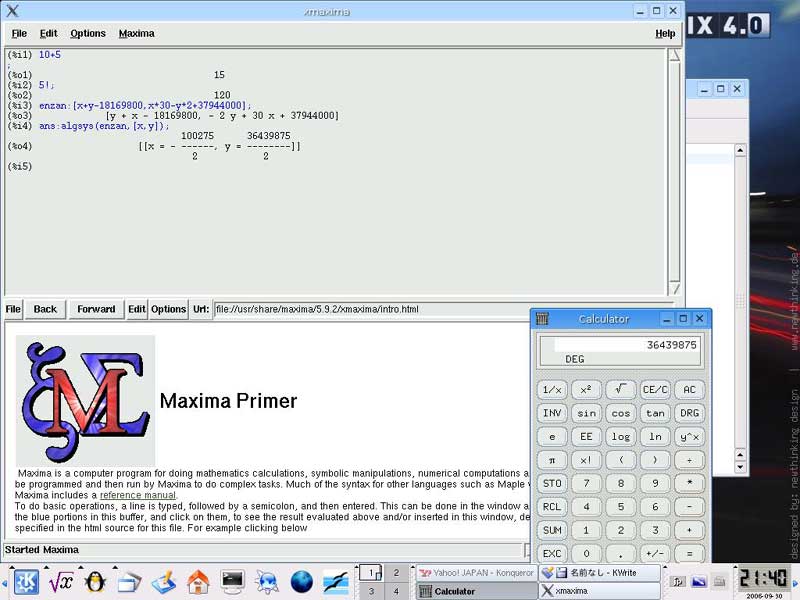 何故か答えの分母が2になってます。(何ででしょ?(^^)) ・・・・・あっ、そうか。 小数点以下を許さないのですね。 なるほど…。 こいつを使えば、二次の連立方程式でも楽々です。 x^2で、x二乗の意味となります…。 「Maxima」については、また今度。 |