![]()
電気・電子回路シミュレータ「LTSpice/Switcher CADⅢ」を使ってみた体験記です。
私もこの度、ちょっと電気なるものを学びたく思いまして・・・。
ですから、完全に素人発進です。
電気音痴の方には、少しは参考になるかも知れません。・・・・・(まだ工事中)
![]()
背景 必要に迫られまして、電気の勉強を開始しました。 実は私、高校時代理系科目を取っていたたものの、当時全然勉強せず、結局文科系出身なんで、ちんぷんかんぷんデス。。。 なんちゅう難しい学問なんや! 電気っちゅうのは! 電気・電子回路シミュレータソフト 「LTSpice/Switcher CADⅢ」というやつが、本に載っていたので、ちょっとやってみました。 ダウンロードはココです。 “No thanks, just download the software. ”というところをクリックしてください。 でも、回路学習の第一歩にはこちらの方が簡単かも知れません。 どこまで使いものになるのか、定かではありませんが。 (抵抗と電池と電球だけあって・・・、他の素子が見当たりません。(笑)) 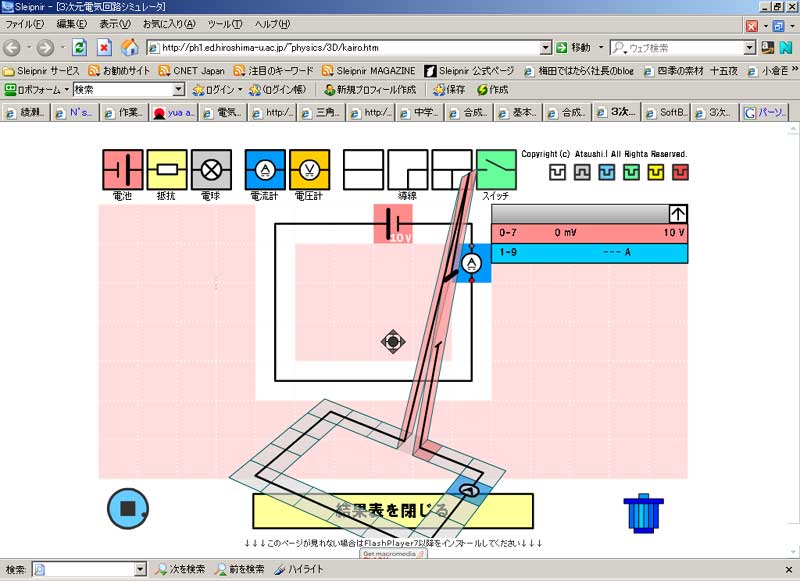 まずは、上のサイトでウォーミングアップ。 電源と電流計のみの回路図です。 この場合、+極と-極との間に10Vの電位差がありますが、抵抗が無いためショートしてしまいます。 “抵抗”とは、電流を通さない為に設けられる素子ですが、初心者は『なんでそんなもん、要るの?』とお思いでしょう。 実は、抵抗が無いと電流をいっぺんに使ってしまい、電源が電池だったりなんかすると、一瞬で電池切れとなってしまいます。 “抵抗”はそれを防ぐ為に、あるんですね。 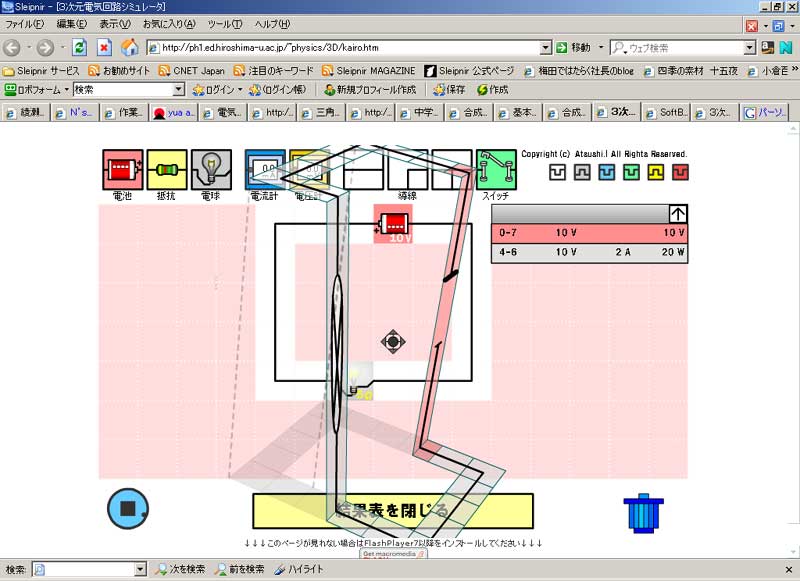 電源と電球のみの回路。 こんなの、小学校2~3年でやりましたね。 豆電球と電池を使って…。 10Vの電源で、5Ωの抵抗。 電流は2Aとなります。(オームの法則より) さて。 「LTSpice/Switcher CADⅢ」をば。 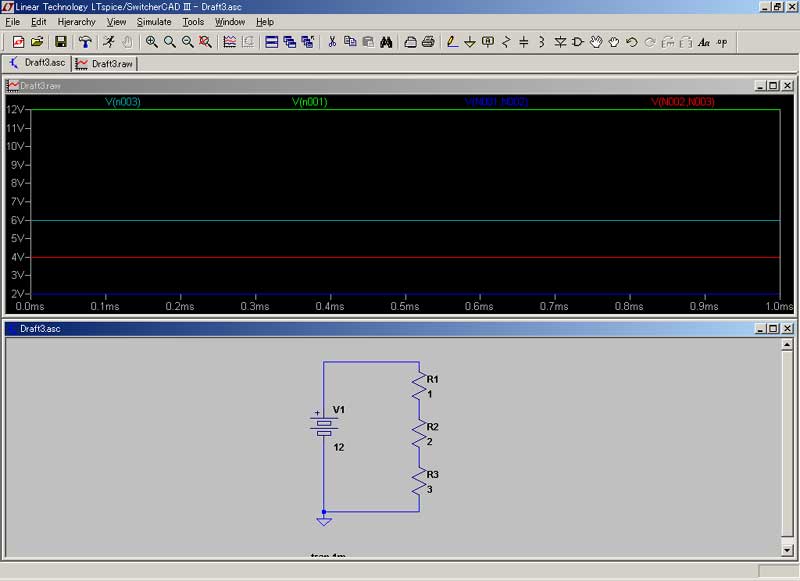 ざっとこんな感じで、ワープロ感覚(CAD感覚?)で、回路図を作成することが出来ます。 うーんとまずは、抵抗を直列に繋ぎました。 R1では12V、R2では6V、R3では4Vと出ます。 なんでそうなるのかと言いますと・・・・。 めんどくさいので、こちらにリンク。(^^) 直列抵抗は、抵抗値を単純に足し算するのですね。 だから、1+2+3で6Ω。 12÷6で、2Aの電流が流れています。(電流は不変です。) 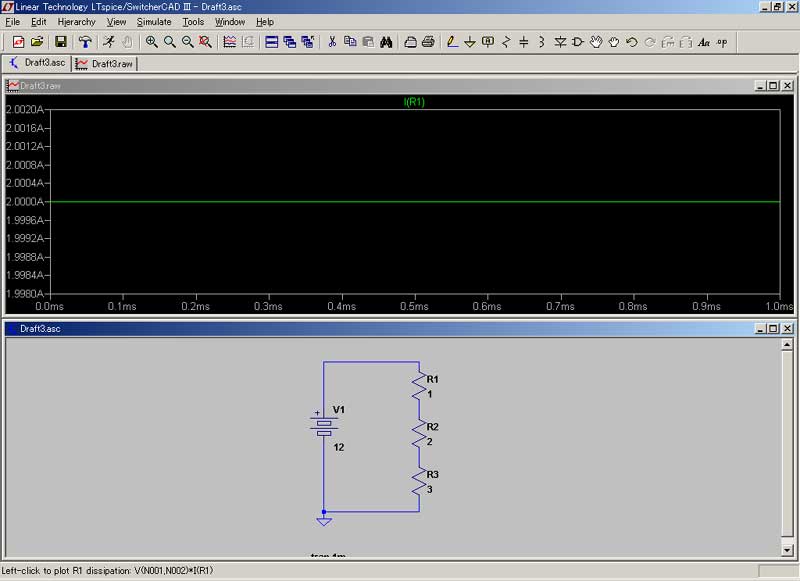 上と同様の回路。 電流はこの場合、一定です。 ほら! 2Aと出てますでしょ? 電流は電圧から抵抗(合成抵抗)を割った値です。 (オームの法則を参照。 ・・・このサイト、中学生向けですね。 中学生でこれですか! すごいなあ。 天才中学生向けサイト、なのでしょうか???) オームの法則が済んだら、キルヒホッフの法則 それから クーロンの法則も覚えておいて損はナイデス。 (クーロンの法則は、万有引力の法則に酷似していますね。) 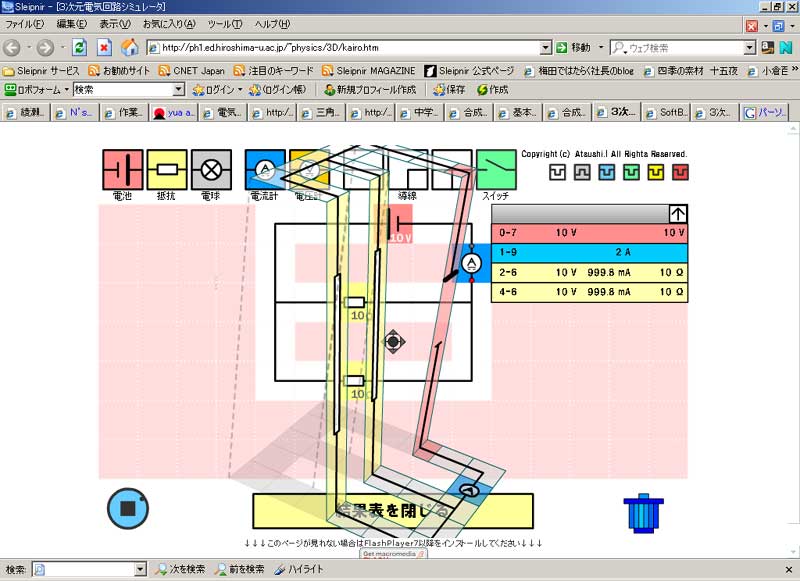 さっきのwebサイトで、並列抵抗を実験してみました。 何で急にこちら(webサイト)になるのかと言うと…。 単なる気まぐれです。(^^) 電源が10V、2つの抵抗がいずれも10Ω。 流れる電流は2Aとなります。 抵抗が並列に並んだときの合成抵抗は、「逆数の和」の逆数となります。 1/10と1/10を足して、2/10。 これを逆数にすると5. 5Ωですね。(和分の積だと、100/20で5Ωです。) 10V÷5Ωで、2Aと出ました。 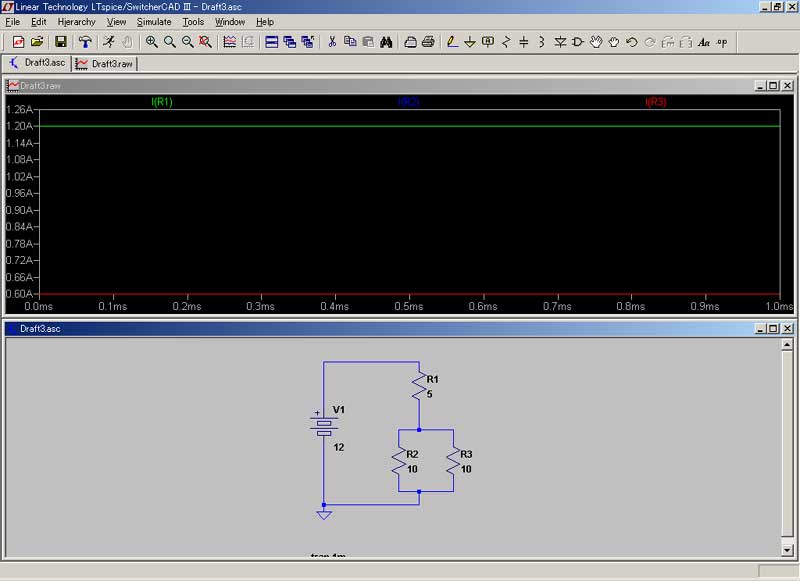 直列と並列が混在したパターン。 1/10 + 1/10 で、2/10 これの逆数が5で、5+5で10となります。 並列の抵抗、つまりはR2とR3の合成抵抗ですが、“和分の積”で算出することも出来ます。(和分の積は、抵抗が2個のときのみ、 使えます。) “和”が20、“積”が100で、100/20で答えが5となります。 5+5で、10となりますね。 ・・・このあたりも、先ほどのサイトに記載がありました。 ほんまに“天才”中学生向けサイトのようです…。 うーむ。 あまりと言えば、あまりに素晴らしいサイトなので、トップページを記させていただきます。 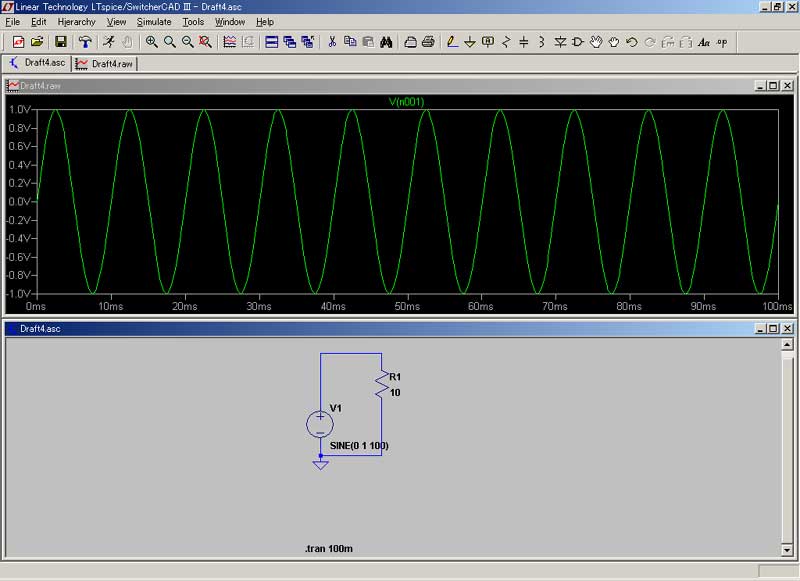 抵抗に交流電源を流したときのシミュレーション。 正弦波となります。 いわゆる、sinカーブですね。 ・・・交流とは何ぞや?の話も、書かないといけないでしょうね。 ま、とりあえずはここでも読んでください。 (意外と、交流を真面目に論じたサイトって、無いようなのです。 確かに難しいですし。 ネットで気軽に読める形式では、 交流を論じることは出来ない、ということでしょうか・・・。) それか、視覚的に解りやすいのがこちら。 ああ、そうそ。 交流は上記のように“波”になってますので、例えばV(ボルト)の値も、時々刻々と変化しておりますデス。 私たち日本の一般家庭の交流電源は、100Vと言われていますね。 これは勿論暫定値でして、実際には+141.42V~-141.42Vまでの間を、ゆらゆらしております…。 (何しろ一定じゃないので。) 交流で言うところのボルト数とは、最大値のことではなく、平均値(実効値)なのです。 でもでも、実はこの“実効値”。 “平均”とは言っても、正確には平均でなかったりします。 だって、上の図を見てくださいよ。 平均を算出するとどんな波でも、平均は0にしか、なりっこないではありませんか! なので、交流の場合、0より下半分を無視することにして、0から最大値までの中間(平均)を、“実効値”とすることになったの です。 でも、そこでまださらに面倒なことがあって、“実効値”を (0+最大値)÷2 で算出するのではなく、最大値÷√2 で求めるの ですね。 これがなんでなのか? 私結構悩みました。 意外や意外。 通常の入門書には、この理由が書かれていないのです。 多分おそらく、本を書いた先生方も、この部分を生徒さんに教えたときの経験から(おそらく意味を理解出来ない生徒さんがいて、 根詰めて教えようと頑張ってみても逆効果になってしまう、みたいな経験をされているのではないかと…。)、『つべこべ言わんと、 そういうものなんや。 そないに思っとけぃ!』で済ました方が無難と、考えてらっしゃるのかも知れません。 (でも、俺が解ったんだから、実のところそんなまで難しい理屈でも無いんですがね…。 何で入門書に書かないんだろ??) 要は、「電力=電流×電圧」 の公式に矛盾しないよう、そうした、というのが正解のようです。 電力を半分にすると、電力の構成要素であるところの“電流”と“電圧”も半分になる、ということだと、おかしなことになってしまい ます。 例えば、最大電力が1000W(電圧100V × 電流10A)なら、実効値が500Wとまあ、半分になりますわな。 電力の実効値が500Wなら、じゃあ電圧も半分で50V、電流も半分で5Aだと(安易に)してしまいますと、50×5で、250Wにしかな らない。 この矛盾を解決するために、電流と電圧はそれぞれ、√2で割ることに決めた(!)ようです。(^^) そうすると、電圧が100÷√2で、70.71。 電流が10÷√2で、7.07。 70.71×7.07で、答えは500になりますね…。 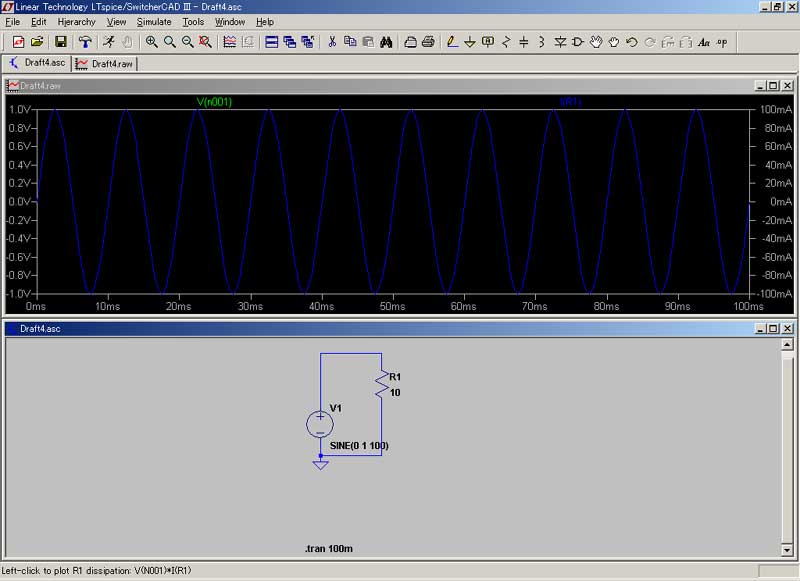 こちらも同じ回路。 今度は電圧ではなく、電流を見ています。 青色の線が映えないのでわかりにくいですが、電流です。 抵抗における電圧と電流は、同相となります。 (同相とは、波の進行が同期していること。 振幅は一致してなくても構いません。 周期が一緒であることを“同相”とし ています。) 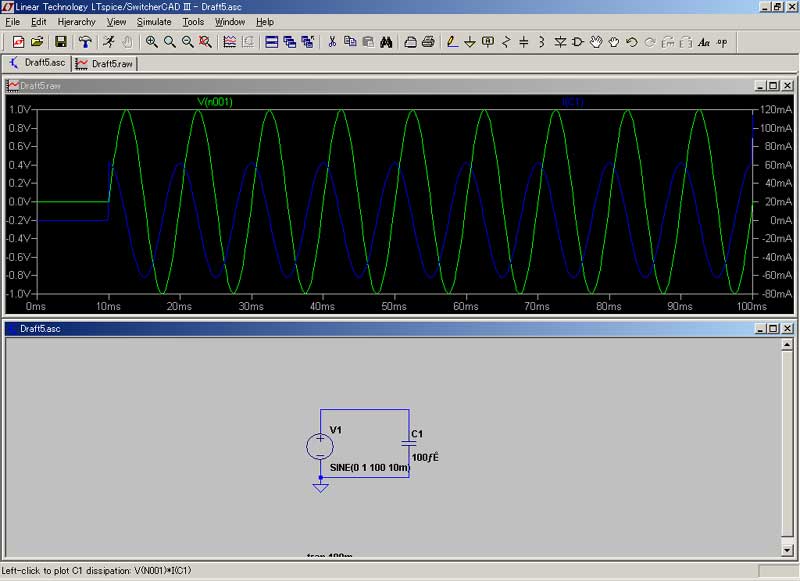 この辺からが、今回の範囲では私が最も興味を抱いたところであります。 コンデンサに交流を流したときの、電圧と電流の波形です。(青色の線があるのが…、見えますでしょうか?) 電流(青の線)が電圧(緑の線)よりも、90°(π/2rad)位相が進んでいます。 このあたりは、もう少し丁寧に解説を試みたいところです。 (コンデンサとは何ぞや?の話も端折ってるし。。。 実際、俺もわからん。(爆)) ・・・ま、コンデンサは直流を蓄え、交流を通すのでした。(*^^*) (コンデンサ間を、実際に電流が流れるわけではなさそうです。 交流の場合、極性が常時反転しており、コンデンサはその都度充放電を繰り返すので、結果、電流が流れているのと同じ ような状態を示すという、どうやらそういうことのようです…。) 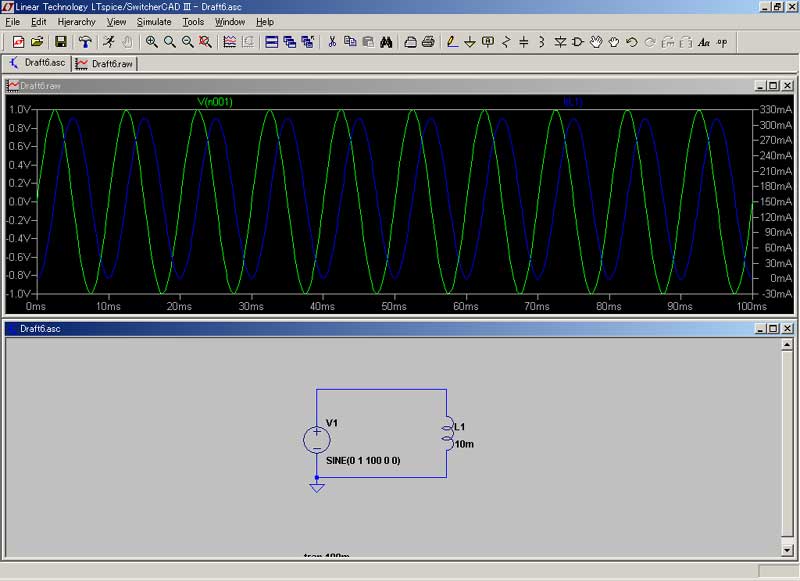 今度は、コイルに交流を流したシミュレーション。(青色の線があるのが…、見えますでしょうか?) 電流が電圧にくらべ、π/2rad(ラジアン)遅れています。(π/2radとは、90°のことです。) うーむ。 「コイルとは何ぞや。」ですか。。。(心許ない。) 導線をグルグル巻きにしたものです。 電気的には、電磁誘導により誘導起電力が生じるので、交流を通しにくくします。 (「レンツの法則」と言って、誘導起電力はコイルを通る磁束の変化を妨げる向きに誘起されるのですね。) 実は“交流”も、電磁誘導と誘導起電力によって生まれているのですけどね。 実はこの「電磁誘導」こそが、“電磁気学のキモ”と言ってよさそうです。 まあ、コイルもコンデンサも、一筋縄ではいかないや。(笑) いやぁ~。 このたび電気を学んでみて、「こんなに難しい分野って、他にあるのかな?」というほどのものを感じました。 「電気やってる人って、天才!!」 いやほんと、そのように感じましたね。 なんたってもう、難しいのなんのって。 どうやら正弦波というのは、結局のところ、等速円運動なんですって。 等速円運動を横から見ると、ピストンが上下に運動しているようにしか見えない。 その「上下運動」に持ってきて、横軸に “時間”という概念を導入してやることにより、正弦波への変換が出来るのですと。 交流におけるキーワードは、“時間”ということに、なるのかも知れません。 この“時間”なるもの…、考えれば考えるほど、不思議な概念でして、このことについて考え出すと、それだけで丸一日潰れ そうなほど、興味深いものが(私には)あります…。 なんて言って、そんなにじっくり考えていられる余裕などないのが実情ですが。 “交流”やってて、思わぬところへ行き着いてしまった。。。 そんでまた、この“位相差”というもんが、これまた興味深いのですねえ。 訳わからんけど面白ソ、とは、このようなことを 言うのでしょうか? 実は、sin(サイン)とcos(コサイン)の関係も、上記の関係と似てるんですなぁ~。(参考) sinの方がcosよりπ/2radだけ、位相が進んでいると。 (中略) 関係ない話はさておき。 でまあ、このπ/2radの位相差を、複素数で表すことが出来ると言うんだから、ほんとにもう、「電気やってる人天才!!」と、私が 思うのも、無理からぬことでしょう…。(^^) 注)複素数とは。 … wikipediaをご参照下さい。 一番上の行だけ読まれればOK。 但しここで、“虚数単位(i)”とは、二乗して“-1”になる数のことを言いますデス。 複素数を複素平面上にプロットいたしまして、その値にi(虚数のこと。数学ではiだけども、物理ではjデス。)をかける と、ちょうどグラフを一象限ずらすような形で、プロットが移動するんですね。 ある複素数“a+bi”に、iをかけると、“ai-b”となって、これ即ち“位相が90°進む。”のと同じことに、なるんではないか! ・・・・・うーん。 「複素平面」とは何ぞや?の話も、欠落しておりますなあ。 でも、高校で習わなかっただけで、そんなに難しいもんじゃありません。(高校で習ったのかな? 俺が覚えてないだけ?) 参考サイトとしては、ちょっと難しいがこのあたり。(←このページの最後に出てくる言葉は、なかなか深遠であります…。) ちょこっと話がそれてしまったけど。 でもってそんな訳で、複素平面のお陰で、複素数を“ベクトル”で言い換えることも可能なんだと。 うーん・・・・・。 ああ、いかんいかん。 そっちの方へ興味が行っちゃうと、電気の勉強でなくなってしまうじゃないか。 ところで先日、「共役複素数」の意味を知らず、数検2級受験者のくせして恥ずかしい思いをした私でしたが、何のことはない。 a+biかa-biかっていう、それだけの話でした。(^^) とまあ、私も数検やってたんで、電気に手を出してみる気になった次第なのですが、もしも数検やってなかったとしたら、とてもとても 太刀打ち出来ず、速攻で諦めているところでした。 やっぱり数学一つでもやると、これまで手を出したくとも出せなかった理系世界が、グンと近づいてきますね。 それはなにげに、良いことだと思いました。 (上の内容も含め、まだまだ全然工事中。) |